Amateur de jardinage, vous désirez ensemencer un bout de terrain dans votre jardin ? Pour réussir dans votre projet, vous devez premièrement identifier le nombre de graines dont vous avez besoin pour couvrir la surface à ensemencer. Pour y arriver, il suffit de calculer l’aire de la surface du bout de terrain. Votre terrain étant triangulaire, vous ignorez comment en déterminer l’aire ? Retour dans ce guide sur l’essentiel à savoir sur le triangle et le procédé mathématique à suivre pour en calculer l’aire de sa surface.
Plan de l'article
Le triangle : l’une des formes géométriques incontournables
En géométrie, on distingue 12 formes. Des classifications permettent de les catégoriser par complexité. D’une part, on retrouve les formes simples et de l’autre on liste les figures les plus complexes. Ces dernières correspondent aux formes géométriques les moins connues. L’ellipse, le trapèze, l’hexagone, l’octogone ou encore le pentagone en sont des illustrations.
A lire également : 5 Conseils pour Réussir sa Stratégie de Content Marketing
Les formes simples sont les figures basiques. Ce sont les incontournables. Elles sont connues de presque tout le monde. Le cercle, le carré, le rectangle et le triangle en sont les meilleurs exemples.
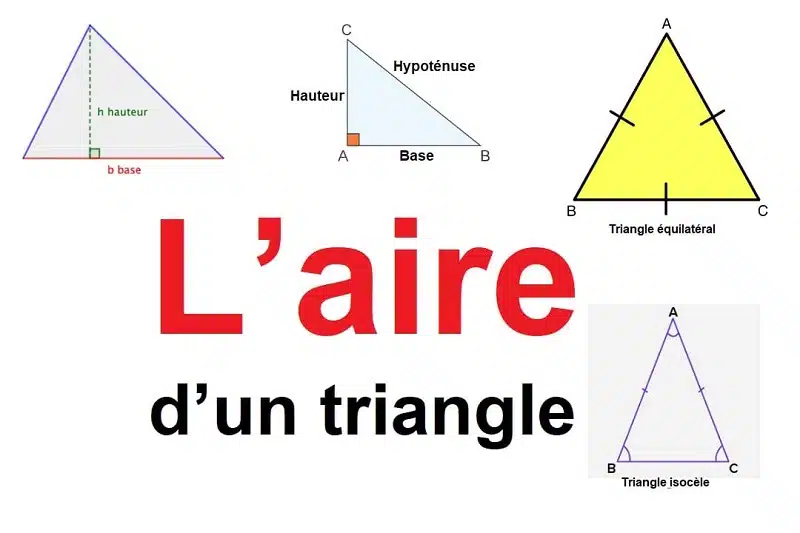
Le triangle, forme à laquelle se consacre ce billet, présente la particularité première de posséder trois côtés. On parle aussi polygone à trois côtés. C’est une figure qui possède trois sommets. Figure plane incontournable, le triangle s’invite assez fréquemment dans la vie courante.
A lire aussi : Dématérialisez et simplifiez votre gestion des notes de frais
Différents types de triangles : l’essentiel à retenir
Avant de nous intéresser au calcul de l’aire du triangle, il est important de préciser que le triangle est une figure qui se décline en plusieurs formes. On distingue notamment 4 grands types de triangles.
- En premier, se présente le triangle équilatéral. C’est un type de triangle dans lequel tous les trois côtés sont de longueur égale.
- En deuxième, on retrouve le triangle rectangle. Dans ce type de triangle particulier, deux des trois côtés forment un angle droit. Les deux autres angles sont alors appelés des angles complémentaires.
- En troisième, se présente le triangle isocèle. C’est un triangle dont deux côtés possèdent la même longueur.
- En dernier, on retrouve le triangle quelconque. Il s’agit d’un triangle qui ne correspond pas aux trois premiers. Les trois côtés sont généralement de longueurs différentes. On parle aussi de triangle scalène. Des subtilités peuvent toutefois être relevées entre le triangle scalène et le triangle quelconque.
Pour précision, un triangle peut présenter des propriétés de plusieurs types. C’est notamment le cas des triangles rectangles isocèles, des triangles rectangles scalènes, etc.
Calcul de l’aire du triangle : voici comment s’y prendre
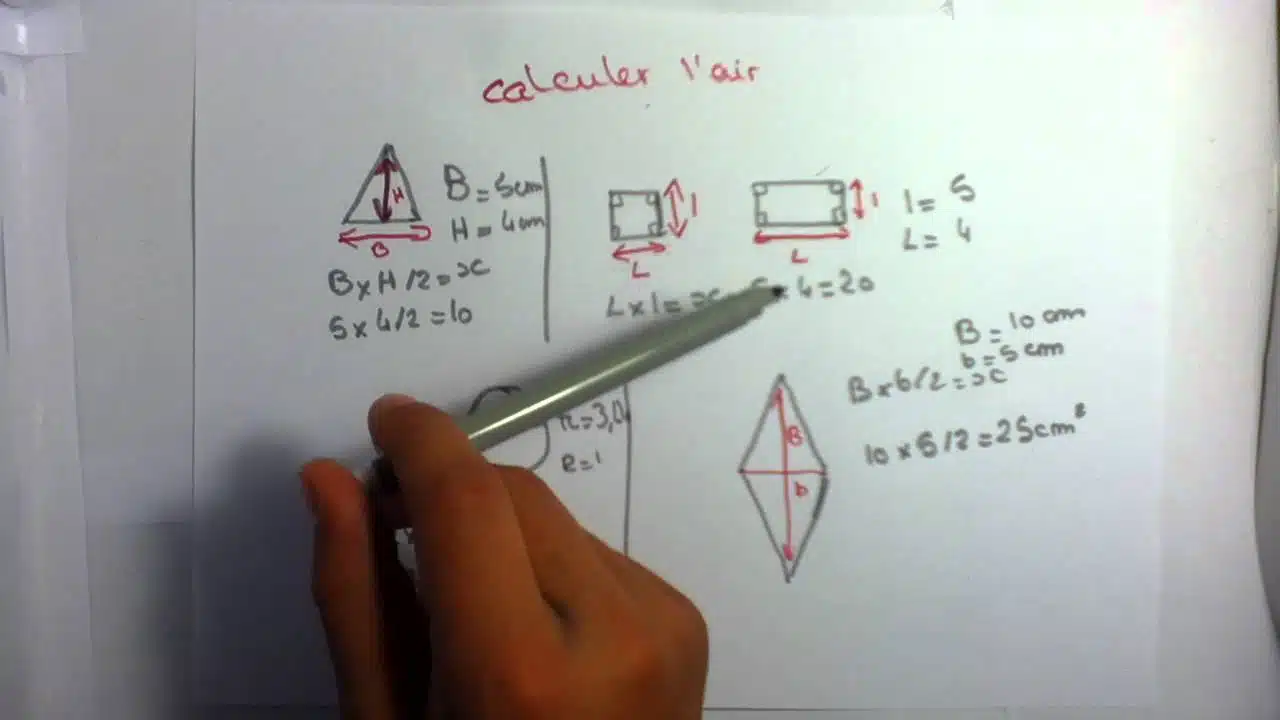
Il est courant de procéder au calcul de l’aire de plusieurs figures. Le triangle ne déroge pas à la pratique. Déterminante, l’aire correspond à la mesure de la surface de la figure géométrique. La valeur est généralement exprimée en centimètres carrés ou en mètres carrés. Pour le calcul de l’aire de chaque figure géométrique, on se sert d’une formule spécifique. Dans le cas du triangle, l’aire correspond au double de la valeur de la base multipliée par celle de la hauteur. La formule mathématique s’écrit : Aire = (b x h) ÷ 2.
Avant de déterminer l’aire du triangle, vous aurez donc besoin de chacune des mesures de ces côtes. La base correspond à l’un des côtés du triangle. La hauteur est la mesure d’une droite. Elle part d’un sommet et est perpendiculaire au côté qui y est opposé. Lorsque les valeurs des deux données sont connues, il suffit d’appliquer la formule pour trouver le résultat.
À titre illustratif, considérons un triangle ayant une base de 10 centimètres et une hauteur de 6 centimètres. Le calcul de son aire correspond alors à (10 × 6) ÷ 2. Le résultat est 30. L’aire de ce triangle est alors égale à 30 centimètres carrés.
Une deuxième formule particulière pour les triangles rectangles
Lorsqu’on est face à un triangle rectangle, il est possible de se servir d’une deuxième formule. Elle est exclusive à ce type de triangle et est tirée de la formule de l’aire du rectangle. L’explication de ce procédé est simple. Un rectangle correspond à deux triangles rectangles. L’aire de la surface d’un triangle rectangle correspond de ce fait à la moitié de l’aire d’un rectangle. Ici, le calcul se concentre sur les deux côtés qui composent l’angle droit du triangle rectangle. Mathématiquement, la formule à suivre est (Longueur × largeur) ÷ 2.
À titre illustratif, considérons un triangle rectangle en C. Le côté AC a une longueur de 9 centimètres tandis que le côté BC a une longueur de 5 centimètres. L’aire de ce triangle rectangle peut se calculer comme ci-après : (9 × 5) ÷ 2. Le résultat est 22,5. L’aire de la surface de ce triangle rectangle est donc de 22,5 centimètres carrés.
Internet : le moyen astucieux de calculer l’aire d’un triangle ?
En dépit des explications de ce guide, vous avez du mal à calculer l’aire d’un triangle ? Inutile de vous inquiéter. Tout est désormais plus simple avec internet. Muni des mesures de la figure, recherchez une calculatrice d’aire de triangle en ligne. Renseignez dans le logiciel les données demandées puis obtenez en un clic l’aire du triangle.
